Spawner-recruit functions

Compute recruitment given spawner abundance, a spawner-recruit function and parameters.

Usage

SR(
  SR_fun = c("BH", "B-H", "bh", "b-h", "Ricker", "ricker", "exp"),
  alpha = NULL,
  alpha_W = NULL,
  alpha_H = NULL,
  Rmax = NULL,
  Rmax_W = NULL,
  Rmax_H = NULL,
  S = NULL,
  S_W = NULL,
  S_H = NULL,
  A = 1,
  R_per_S = FALSE
)

Arguments

SR_fun: One of "exp" (density-independent discrete exponential), "BH" (Beverton-Holt, the default), or "Ricker", indicating which spawner-recruit function to fit. Synonyms "DI", "B-H", "bh", "b-h" and "ricker" are accepted.
alpha: Numeric vector, matrix, data frame, posterior::rvar(), or draws of intrinsic productivity (i.e., recruits per spawner at zero spawner density; slope of the spawner-recruit function at the origin).
alpha_W, alpha_H: Numeric vectors, matrices, data frames, posterior::rvar() or draws of intrinsic productivity for wild- and hatchery-origin spawners, respectively. If they differ, both must be specified and alpha must not be used (and conversely).
Rmax: Numeric vector, matrix, data frame, posterior::rvar(), or draws of maximum recruitment per unit of habitat (length or area). This corresponds to the asymptote of the Beverton-Holt or the mode of the Ricker.
Rmax_W, Rmax_H: Numeric vectors, matrices, data frames, posterior::rvar() or draws of maximum recruitment per unit of habitat for wild- and hatchery-origin spawners, respectively. If they differ, both must be specified and Rmax must not be used (and conversely).
S: Numeric vector, matrix, data frame, posterior::rvar(), or draws of spawner abundance.
S_W, S_H: Numeric vectors, matrices, data frames, posterior::rvar() or draws of wild- and hatchery-origin spawner abundance, respectively. Must be specified if either alpha or Rmax differ by rearing type, in which case S must not be used (and conversely).
A: Numeric vector, matrix, data frame, posterior::rvar(), or draws of spawning habitat size (either stream length or area), used to standardize Rmax. The default is 1, in which case Rmax is in units of abundance (which is also density).
R_per_S: Logical indicating whether to return recruits per spawner rather than recruits (the default).

Value

A vector, matrix, data frame, posterior::rvar() or draws, depending on the argument types, containing either recruits or recruits per spawner. Calculations are vectorized and elements of shorter arguments are recycled as necessary.

Details

The salmonIPM package uses a nonstandard parameterization of the Ricker model by the maximum recruitment Rmax. This is typically better identified by data than per capita density dependence, and it facilitates a common interpretation and priors with the Beverton-Holt. Here \(e\) is the base of the natural logarithm.

Note that the functions for the RRS != "none" case are written below in their most general form, with both alpha and Rmax differing between wild and hatchery spawners. If only one parameter is specified in RRS, then the _W and _H values of the other parameter are equal and the expression can be further simplified.

RRS == "none"

\( R = \begin{cases} \alpha S & \text{exponential} \\\\ \dfrac{\alpha S}{1 + \dfrac{\alpha S}{A R_\text{max}}} & \text{Beverton-Holt} \\\\ \alpha S \text{exp} {\left(- \dfrac{\alpha S}{e A R_\text{max}} \right)} & \text{Ricker} \end{cases} \)

RRS != "none"

\( R = \begin{cases} \alpha_\text{W} S_\text{W} + \alpha_\text{H} S_\text{H} & \text{exponential} \\\\ \dfrac{\alpha_\text{W} S_\text{W} + \alpha_\text{H} S_\text{H}}{1 + \dfrac{\alpha_\text{W} S_\text{W}}{A R_\text{max,W}} + \dfrac{\alpha_\text{H} S_\text{H}}{A R_\text{max,H}}} & \text{Beverton-Holt (Leslie-Gower)} \\\\ \left(\alpha_\text{W} S_\text{W} + \alpha_\text{H} S_\text{H} \right) \text{exp}\left(-\dfrac{\alpha_\text{W} S_\text{W}}{e A R_\text{max,W}} - \dfrac{\alpha_\text{H} S_\text{H}}{e A R_\text{max,H}} \right) & \text{Ricker} \end{cases} \)

Examples

alpha <- 3
Rmax <- 1000
S <- 500

# default is Beverton-Holt
SR(alpha = alpha, Rmax = Rmax, S = S) 
#> [1] 600

# approximately Rmax
SR(alpha = alpha, Rmax = Rmax, S = 1e6) 
#> [1] 999.6668

# scale Rmax by habitat area
SR(alpha = alpha, Rmax = Rmax, S = S, A = 0.1) 
#> [1] 93.75

# discrete exponential ignores Rmax
SR(SR_fun = "exp", alpha = alpha, Rmax = Rmax, S = S) 
#> [1] 1500

# vectorization with recycling
SR(alpha = rep(alpha, 10), Rmax = rep(Rmax, 10), S = matrix(S, 10, 4)) 
#>       [,1] [,2] [,3] [,4]
#>  [1,]  600  600  600  600
#>  [2,]  600  600  600  600
#>  [3,]  600  600  600  600
#>  [4,]  600  600  600  600
#>  [5,]  600  600  600  600
#>  [6,]  600  600  600  600
#>  [7,]  600  600  600  600
#>  [8,]  600  600  600  600
#>  [9,]  600  600  600  600
#> [10,]  600  600  600  600

# return recruits per spawner
SR(alpha = alpha, Rmax = Rmax, S = S, R_per_S = TRUE) 
#> [1] 1.2

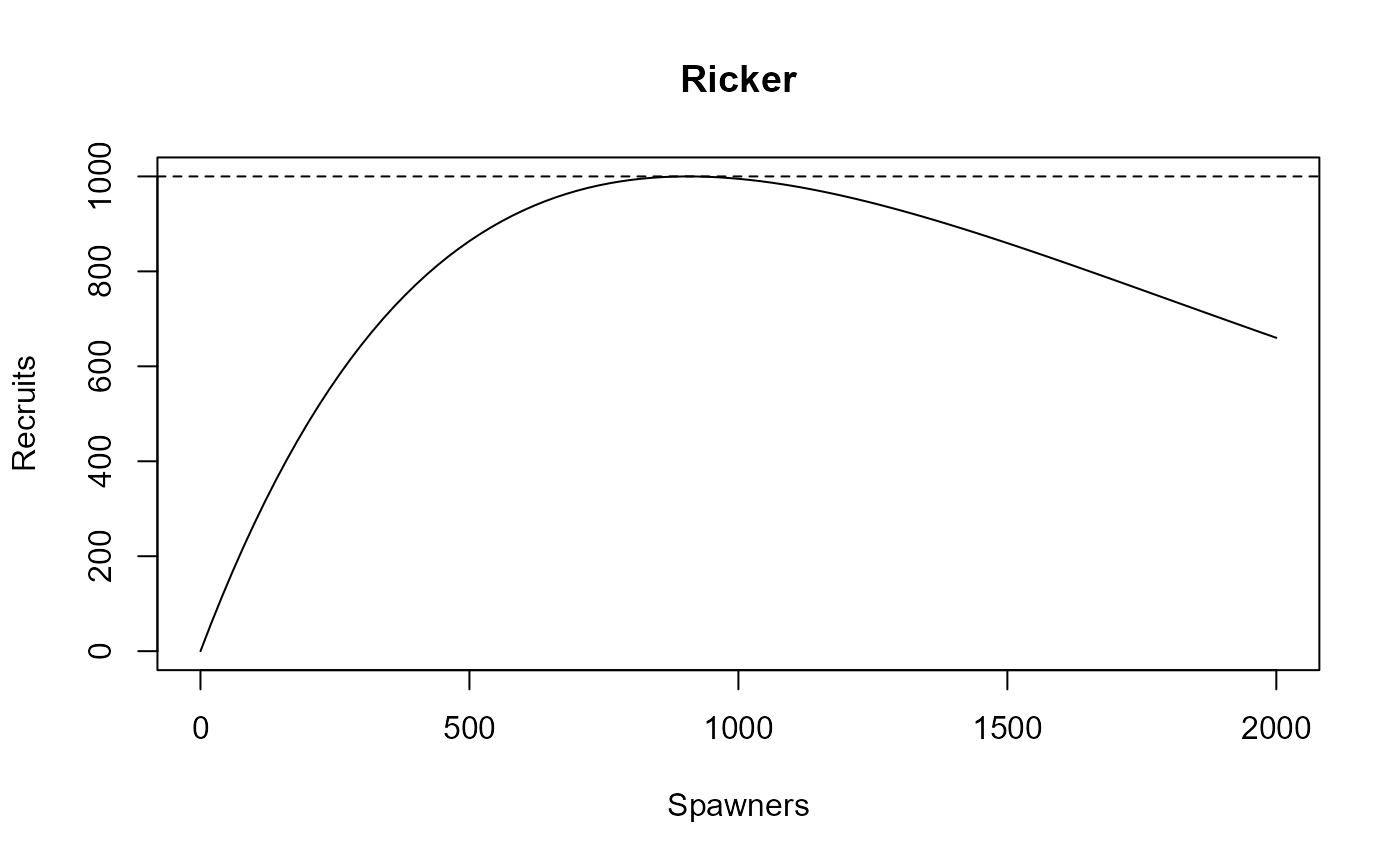
# plot Ricker and show Rmax
curve(SR(SR_fun = "Ricker", alpha = alpha, Rmax = Rmax, S = x), from = 0, to = 2000,
      xlab = "Spawners", ylab = "Recruits", main = "Ricker")
abline(h = Rmax, lty = 2)


# differential hatchery / wild relative reproductive success
alpha_W <- 3
alpha_H <- 2
S_W <- 400
S_H <- 100
# compare to BH result above
SR(alpha_W = alpha_W, alpha_H = alpha_H, Rmax = Rmax, S_W = S_W, S_H = S_H)
#> [1] 583.3333

Usage

Arguments

Value

Details

See also

Examples